有两题理解的不够透彻，还有两题是水题，先贴A和F了。

https://vjudge.net/contest/421531

A.DP

A - Tetrahedron

You are given a tetrahedron. Let’s mark its vertices with letters A, B, C and D correspondingly.

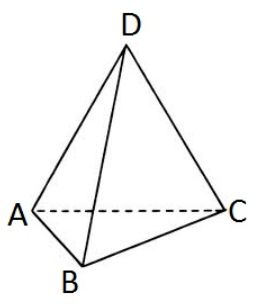
An ant is standing in the vertex D of the tetrahedron. The ant is quite active and he wouldn’t stay idle. At each moment of time he makes a step from one vertex to another one along some edge of the tetrahedron. The ant just can’t stand on one place.

You do not have to do much to solve the problem: your task is to count the number of ways in which the ant can go from the initial vertex D to itself in exactly n steps. In other words, you are asked to find out the number of different cyclic paths with the length of n from vertex D to itself. As the number can be quite large, you should print it modulo 1000000007 (109 + 7).

Input

The first line contains the only integer n (1 ≤ n ≤ 107) — the required length of the cyclic path.

Output

Print the only integer — the required number of ways modulo 1000000007 (109 + 7).

Examples

Input

2

Output

3

Input

4

Output

21

题意

从三棱锥的一个顶点D出发，要求走n步后能回到出发点D，问有多少种走法，对结果取1e9+7的模。

分析

dp问题。设dp[i]为走i步的答案。要求走i步时，由于第i-1步必定不在D点，所以如果知道dp[i-2]，从其出发走向任意一点，再回到D点即可。该情况只包含第i-2步在D点，还有第i-2步不在D点的情况。保证第i-2步不在D点，只需保证i-1步在D点即可。即dp[i-1]. 知道dp[i-1]的情况下，其退一步会回到A、B、C三点中的一点。此时再任意走向非D的点即可，得到状态转移方程：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
typedef long long ll;
int main()
{
	int n;
	cin >> n;
	ll dp[n + 1];
	dp[1] = 0;
	dp[2] = 3;
	for(int i = 3; i <= n; ++i){
		dp[i] = (dp[i - 1] % mod * 2 + dp[i - 2]  % mod * 3) % mod;
	}
	cout << dp[n];
	return 0;
}

F.思维

F - Jumping Jack

Jack is working on his jumping skills recently. Currently he’s located at point zero of the number line. He would like to get to the point x. In order to train, he has decided that he’ll first jump by only one unit, and each subsequent jump will be exactly one longer than the previous one. He can go either left or right with each jump. He wonders how many jumps he needs to reach x.

Input

The input data consists of only one integer x ( - 109 ≤ x ≤ 109).

Output

Output the minimal number of jumps that Jack requires to reach x.

Examples

Input
2
Output
3

Input
6
Output
3
Input
0

Output
0

题意

从坐标0点出发，第一次跳跃能跳1格，此后每一次跳跃都能多跳一格，输入一个x，问最少多少步能跳到x。

分析

第一眼看到题的时候是想的dfs求最短步数，结果数据来了个±1e9，直接死掉了……

然后分析找规律，首项1，公差1的等差数列和的所有正负坐标都可以直接求出。除此以外，如果直接往右走，无法达到x，就取直接往右走的情况下x右边第一个能走到的坐标。此时，x在两个能直接往右走达到的坐标之间，设x与其右边能走到的点距离为d，若这个距离d是偶数，那么只需要改变前面某个特定一步的方向即可。例如，要走到坐标4，直接往右走，能走到1，3，6这几个点，6与4的距离是2。于是我们找：走到6点的过程是0+1+2+3，我们翻转其中的第1步，变成0-1+2+3，于是就走到坐标4了。

简单证明一下：因为步长中，相邻的两项一定是一奇一偶，相加得到奇数，而如果把其中较大的变为相反数，相加就是-1，那么这两个和的差是奇数+1，一定是一个偶数。

再讨论d为奇数的情况。遇到d为奇数时，我们只需要走到和为偶数的情况即可。这个时候看我们走的是第几步，如果我们这一步下去是一个奇数，那么距离就会变成一个偶数，所以我们只需要原步数+1即可。反之，我们需要原步数+2.

另外由于左右对称，我们把x取绝对值即可。

综上，当x是首项为1，公差为1等差数列和数列的第n项时，步数是n；如果不是n，让n+1，求出这个和值，并计算d；如果d是偶数，步数仍然是n；如果d是奇数且n是奇数，步数是n+1；如果d是奇数且n是偶数，步数是n+2.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
signed main()
{
	ll x;
	cin >> x;
	x = abs(x);
	int n = 0;
	while(n * (n + 1) / 2 < x) n++;
	if(n * (n + 1) / 2 == x) cout << n;
	else{
		if((n * (n + 1) / 2 - x) % 2 == 0){
			cout << n;
		}
		else if((n + 1) % 2 == 0){
			cout << n + 2;
		}
		else cout << n + 1;
	}
	return 0;
}