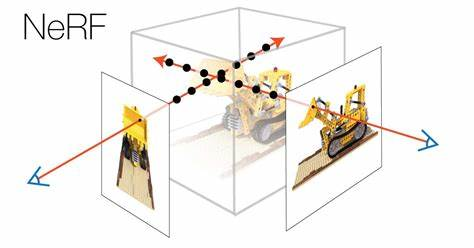
BRDF 和 Blinn-Phong

了解 BRDF — 标准光照模型
BRDF 是真实化渲染一个重要的模型。以下实现的各种渲染方法都将符合 BRDF 的规则。
首先可以参考这篇论文:A Basic Introduction to BRDF-Based Lighting
(((
在了解渲染方法之前,你应该首先知晓渲染管线的基本流程。
标准光照模型 - BRDF (Bi-directional Reflectance Distribution Function,也称双向反射模型) 是一种广泛用于图形渲染的光照模型。它的基本方法是将进入摄像机的光分为四部分:
自发光、高光反射、漫反射 和 环境光.
- 自发光 (emissive) 即物体本身向摄像机辐射的光(而非折射/反射)。如果你没有使用全局光照技术,自发光并不会让物体看起来在发光,而只是亮度提高了。使用全局光照后,自发光的物体可以影响附近物体的光照。
- 高光反射 (specular) 即模型向摄像机完全镜面反射的光强。
- 漫反射 (diffuse) 即模型接收到光照后,向所有方向反射的光强。该值与视角无关。
- 环境光 (ambient) 除以上三点以外的所有其他光照。这些一般都是间接光照。例如前面提到的全局光照。环境光一般是必须的,如果没有环境光,没有受到光源直线照射的地方将完全黑暗,这是不符合实际的。(在素描中也学过,暗面和阴影的交界处是有些许反光的)
最后一个片元呈现的颜色就是这四种光的线性和。
除开双向反射模型以外,还有一种双向透射模型(BTDF),一般用于表现透明材质。二者统称为双向散射模型(BSDF)。
漫反射光照的兰伯特定律
兰伯特定律的表述很简单:
如上公式, $I$ 为光强,$\vec n, \vec l$ 分别为归一化后的表面法向量和光照方向,如下图所示(图来自《Unity Shader 入门精要》):

其中,$k_d$ 是漫反射系数,由材质颜色乘以光线强度得到。
那么公式的意义实际上就是说漫反射的光强与法线和光源方向夹角的余弦值成正比(因为 $\vec n · \vec l=cos(\vec n, \vec l)$)。这和我们的感性认识——表面的角度偏离光源越远光照越少,是一致的。
这一定律在各种 Shading methods 中广泛使用。
下面来看看基于 BRDF 的经验模型是如何实现的。
Phong Shading & Gouraud Shading
冯(Phong)着色与高洛德(Gouraud)着色都是最经典的经验 Shading. 而且着色算法也是一样的。唯一的不同就是:Phong Shading 是在片元着色器阶段对每一个片元操作的,而 Gouraud Shading 是对顶点操作的。下面根据 BRDF 的四个光照部分来引入这两种 Shading 的公式。
漫反射
漫反射部分直接使用 Lambert law 即可:
其中,将漫反射颜色 $m_{diffuse}$ 与光照强度 $c_{light}$ 相乘,并保证漫反射取正值,这样可以防止物体在背光处被光源直接照亮。
高光反射
还是本文第一张图,Phong 模型通过如下公式计算高光反射:
其中,$\vec v$ 为视线向量,$\vec r$ 是反射方向向量。
不过,对于高光的计算,还有另一种经验计算方法—— Blinn 模型,它使用一个新的矢量 $\vec h=normalize(\vec {v + l})$ ,公式为
其实 Phong 模型和 Blinn 模型高光计算方法都是经验模型,在不同的情况下有不同的表现,不一定 Phong 更加符合实验结果。而 Blinn 的区别主要在于,当视角不动时,其计算的 $\vec h$ 几乎是一个常量,由此节约了性能。而在高速移动的视角下 Phong 模型也许更快。
总之,使用 Blinn 高光算法的模型一般也称为 Blinn-Phong Shading.
环境光
对于简单的 Blinn-Phong 模型,环境光给一个全局常量即可(敷衍就行了)。例如在 Unity Shader 中,你可以把 UNITY_LIGHTMODEL_AMBIENT 拿来当环境光。
自发光
和环境光一样,自发光也只使用一个固定常数。
总之,Blinn-Phong 模型只是一个经验模型,很多地方都做得很简单。和真实的物理光照是不同的,但表现出来的效果可以八九不离十。这也就是某一般路过(误)邓恩(3D Math Primer For Graphics And Game Development 的 writer)提出的图形学第一定律所说:
如果它看起来是对的,那么它就是对的。
如果你将以上过程应用到顶点着色器而不是片元着色器,那么你会得到一个更粗糙的着色效果,也就是 Gouraud Shading.
下面是不含高光部分的代码实现。
1 | // Gauraud |
高光如何实现呢?
且回看上方高光公式。简单地加一个高光向量:
1 | fixed3 specular = _LightColor0.rgb * _Specular.rgb * pow(max(0, dot(v.worldNormal.xyz, halfDir)), _Gloss); |
这里采用的是 Blinn 方法, _Specular 是高光的颜色向量。另外,halfdir 的计算:
1 | fixed3 halfDir = normalize(worldLightDir + viewDir); |
最后和 ambient + diffuse 直接相加。
Half-Lambert
普通的 Lambert 方法处理的背光面会出现和真实情况相差甚远的情况——整个背光面都是黑的,没有亮度差别。而在实际观察中,即使是背光面也是存在量不同的反光的,只使用一个统一的环境反射光来表现显然不能解决问题。
问题的出现是因为使用的公式是 saturate(dot(worldNormal, worldLight),对点积小于 0 的部分直接舍去用 0 代替,背光面出现大量亮度都为 0 的片元。
所以对 Lambert 进行一个重新取值,公式修改为
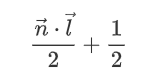
对比如下:


不管怎样,两种渲染方式都缺少明暗交界线,是经验模型下单光源光照的缺点。