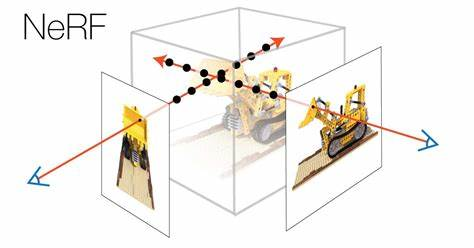
NeRF:Representing Scenes as Neural Radiance Fields for View Synthesis 阅读与复现
Part. 1 翻译
*使用带位姿信息的神经辐射场表示场景
摘要
NeRF 使用一个全连接的深度网络表示场景,输入为连续的 5D 坐标,输出为该位置的体积密度和视角相关的辐射强度。
NeRF 方法通过查询射线的 5D 坐标合成视角,使用经典的体积渲染技术输出颜色和密度,投影到图像中。体积渲染可导,通过这一点可以优化表示,使得只需要使用一组有已知相机姿态的图像作为输入。
本文还探讨了如何继续优化神经辐射场来渲染具有复杂几何外形的场景,与前人工作进行了比较。
1. 引言
给定一组输入图像及相应的相机姿态生成场景新视角。
要正确输出逼真的场景,必须正确处理复杂的几何形状和材质反射特性。
现在我们需要一个能在大范围相机基线上实现逼真质量场景还原的方法。
(总之,我们提出了一种高质量且高性能的神经渲染方法)
实现:将静态场景输入表示为一个 5D 函数 $(x,y,z,\theta,\phi)$,输出为(1)每个点上的密度 $\rho$,密度充当不透明度,表示光线穿过 $(x,y,z)$ 积累的辐射强度、(2)视角相关的 RGB 颜色。通过优化一个深度全连接神经网络来不使用卷积去表示模型。
推理步骤:
- 沿相机射线生成一系列 3D 采样点。
- 使用对应的 2D 观察方向作为输入,生成一组输出颜色和密度。
- 使用体积渲染技术将输出积累到 2D 图像中,可以使用梯度下降法优化。
即这一过程中需要先使用一个多层全连接神经网络输出三维点的密度和颜色,再使用体积渲染还原为 2D 图像。
问题1:
该表示无法收敛到足够高的分辨率。需要使用 5D 坐标进行位置编码。
问题2:
使用体素/网格方法,存储成本非常大。需要使用神经网络的参数来存储场景信息。
2. 相关工作
近期(2019~2020)三维重建中的一个研究热点是将物体和场景编码到 MLP 的权重中来隐式表达 3D 空间位置映射。但是这种方法难以准确精细。
NeRF 增强了神经场景表示的能力,以产生渲染复杂逼真场景的最先进结果。
2.1 神经 3D 形状表示
近期许多研究将$(x,y,z)$ 映射到有符号距离函数或占据场的深度网络。但是这些模型受限于对真实 3D 几何形状的要求(Occupancy Networks 的强分类关联),使得数据集通常需要从诸如 ShapeNet 之类的 baseline 中获取。之后的研究通过构建可微分渲染函数来放宽对真实 3D 形状的要求,使得神经隐式形状表示可以使用 2D 图像进行优化。Niemeyer 等人将表面表示为占据场,并使用数值方法找到每条射线的表面交点,然后使用隐式微分计算精确导数。每个射线交点位置作为输入提供给一个神经 3D 纹理场,该场预测该点的漫反射颜色。Sitzmann 等人使用一个不那么直接的神经 3D 表示方法,简单地在每个连续的 3D 坐标处输出一个特征向量和 RGB 颜色,提出了一个由递归神经网络组成的可微分渲染函数,该函数沿着每条射线前进以确定表面的位置。
这些研究可能足够用于表示复杂高分辨率几何形状,但仍然限制在简单几何形状上,导致复杂结果渲染过于平滑。
我们的解决方法是通过优化网络来编码 5D 辐射场。可以表示更高分辨率、更复杂的的几何形状。
2.2 视角合成和基于图像渲染
使用基于网格的场景表示,可微光栅化器和可微路径追踪器可以直接优化网格表示,通过梯度下降重现一组输入图像。但基于图像投影的基于梯度的网格优化通常很困难,可能是由于局部最小值或损失函数表面的糟糕条件。而且这种方法通常固定拓扑结构,难以对于无约束真实场景通用。
另一种方法使用体积表示来解决问题。体积表示法能够逼真表示复杂形状材质,非常适合基于梯度优化,并且产生更少的伪影。早起体积方法观察图像后直接为体素网格上色。近期的方法使用大量包含多个场景的数据集来训练深度网络,从一组输入图像预测采样的体积表示,然后在测试时使用 alpha 合成或沿射线学习来渲染新视角。
还有一些工作将 CNN 和体素网格结合优化,使得 CNN 可以弥补来自低分辨率体素网格的离散化伪影,允许预测体素网格根据输入时间或动画控制而变化。但这些研究在扩展到更高分辨率图像方面的能力还是受到离散采样的制约——时间和空间复杂度非常高。
我们通过深度全连接神经网络中参数编码连续体积来绕过这个问题,产生了比以往体积方法更高质量的渲染结果,而存储成本只有体积表示的一小部分。
3. 神经辐射场的场景表示
输入为 5D 向量函数 $(x,y,z,\theta,\phi)$,输出为 $c\sigma$($(r,g,b)$ 和体积密度 $\sigma$)。在实践中,我们将方向表示为 3D 笛卡尔单位向量 $d$,使用 MLP 网络表示如下函数:
近似这个连续的 5D 场景表示,并优化权重 $\theta$,使得每个输入能映射到相应体积密度和方向发射的颜色。
为了让网络能在多视角下尽量保持一致性,我们限制网络将体积密度 $\sigma$ 预测仅为与 $(x,y,z)$ 有关的函数,然后让位置和视角 $(\theta,\phi)$ 去共同决定颜色输出 $c$. 为了实现这一点,$F_\theta$ 首先使用 8 个全连接层,每层使用 ReLU 激活 + 256通道)处理输入的三维坐标,并输出 $\sigma$ 和一个 256 维的特征向量。然后将特征向量与相机射线的视角方向进行拼接,传递给一个额外的全连接层(ReLU 激活,128 通道),输出视角相关的 RGB 颜色。
我们可以用输入的视角方向来表现一些不符合兰伯特定律的图形。
4. 辐射场体渲染
5D 神经辐射场将场景表示为空间中各个点的体密度和方向辐射强度。使用经典体积渲染原理来渲染穿过场景的任意射线的颜色。
体积密度 $\sigma(x)$ 可以被解释为射线在位置 $x$ 处终止于无穷小粒子的微分概率。相机射线 $r(t)=o+t_d$ 的期望颜色 $c(r)$(其中 $o$ 是相机位置,$d$ 是射线方向,$t$ 是参数化射线的参数,近截和远截参数分别为 $t_n$, $t_f$,颜色的计算公式如下:
$$ C({\bold r})=\int_{t_n}^{t_f}T(t)\sigma({\bold r}(t))c({\bold r}(t),{\bold d}){\rm d}t $$,其中 $T(t)=\exp{(-\int_{t_n}^t\sigma(\bold r(s)){\rm d}s)}$.
函数 $T(t)$ 表示 $t_n$ 到 $t$ 的累积透射率,即射线在 $t_n$ 到 $t$ 的路径上没有与其他粒子碰撞的概率。从我们的连续神经辐射场渲染视图,对通过所需虚拟相机的每个像素跟踪的相机射线估计积分 $C(r)$. 使用数值积分方法(蒙特卡洛积分)来对这个连续积分进行估计。确定性积分方法通常用于渲染离散化的体素网格,但使用体素方法会极大限制分辨率。作为替代,我们使用分层抽样,将 $[t_n,t_f]$ 划分为 $N$ 个均匀间隔区间,然后在每个区间内均匀抽取一个样本。
$$ t_i\sim u\begin{bmatrix}t_n+{{i-1}\over N}(t_f-t_n),t_n+{i\over N}(t_f-t_n)\end{bmatrix}. $$这样,尽管我们使用的是离散样本集,但分层抽样使得我们能够表示连续场景,这是因为在优化过程中,MLP 会在连续的位置进行评估(为什么呢)。我们使用这些样本,使用 Max 等人在体积渲染综述中提出的求积法则来估计 $C(r)$.
,其中 $\delta_i=t_{i+1}-t_i$,为分层取样点的间距。
使用 $c_i,\sigma_i$ 来计算 $\hat C(\bold r)$ 是可微的,并且可以简化为传统 alpha 合成,其中$\sigma_i=1-\exp(-\sigma_i\delta_i)$.
5. 优化神经辐射场
为了实现高分辨率复杂场景的表示,我们需要两个改进措施。
(1)对输入坐标进行位置编码,帮助 MLP 表示高频率函数。
(2)使用层次体积抽样。
5.1 位置编码
5.2 层次抽样
6. 结果
Part. 2 问题
摘要
什么是体积渲染技术?
体积渲染即神经渲染,相较于原来的光栅化/光线追踪,使用神经网络进行逆向渲染.
辐射场体渲染
公式 $(3)$ 中的 $u$ 是什么?
$u$ 指代均匀分布。
MLP 连续评估的原理?
文中所指的 alpha 合成是什么?好像并不是前景合成透明图片?
Part. 3 理解分析
NeRF 使用的重要概念之一,神经辐射场,其数据形式即 $(c,\sigma)$,使用如下模型隐式表达:
然后看公式 $(2)$,
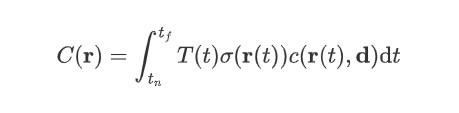
其中 $T(t)$ 通俗点讲就是 $t$ 之前没有碰到粒子的概率,$\sigma(t)$ 表示 $t$ 处碰到粒子的概率。
$T(t)=\exp{(-\int_{t_n}^t\sigma(\bold r(s)){\rm d}s)}$,$r(t)=o+t_d$.
再看公式 $(3)$. 因为实际用计算机计算时还是只能使用离散采样,因此我们要选择一个采样方法,$(3)$ 即 NeRF 采用的方法。这个很好理解,就是$[t_n,t_f]$ 的 $N$ 个均匀离散点。
然后得到 $C(r)$ 的离散近似估计,即公式$(4)$.
这里把 $T(t)$ 换成离散的 $T_i$,$\int\sigma({\bold r}(t)){\rm d}t$ 换成 $\sum\exp(-\sigma_i\delta_i)$, $c(r(t),d)$ 换成 $c_i$(该离散点期望的颜色)。
然后是两个对求 $C(r)$ 的优化。
MLP 倾向于学习低频信息,导致渲染表示颜色和几何图形的高频变化方面表现得比较差。作者还表明,在将输入传递到网络之前,高频函数可以将输入映射到更高维空间,更好你和包含高频变化的数据。
因此,优化之一是转而使用位置编码,令 $F_\theta=F_\theta’·\Gamma$. 其中 $\Gamma$ 为位置信息。
可以参考一下 Transformer 模型的编码方式.
二是分层采样。沿着每个相机光线在 $N$ 个查询点密集评估辐射场网络效率很低:自由空间和已经被遮挡的区域都被采样了。使用分层采样可以缓解这一问题。即一开始使用粗采样,然后计算预期颜色。
Part. 4 复现
用 autodl 跑示例代码。