2021寒假训练第一周解题报告
前言:换了主题之后WP的傻瓜文本编辑器也没了,所以在RealsaltedFish的指路下搞了个Typora来写Markdown文本。html果然还是太复杂了啊ヽ( ̄▽ ̄)ノ
正文,首先贴训练链接:
Div3专题
DFS/BFS专题(以前练过,应该不会写题解了)
DP专题
贪心算法专题好了,贴完链接,惭愧地说我只有Div3专题能写题解,怎么说呢,搜索专题是懒了,贪心是已经很努力在贪了,但是基本上一题能贪一天(是我不够贪心呜呜呜呜),动规的话,打算这周先熟悉好二叉树,下周再看进阶动规,是这样的 我舅要写!舅要写!
因为水题不在少数(当然完全不会做的也更多),所以只贴一部分题。
专题训练结束后贴一贴其他题题解,也算回顾一下。
Div3专题
E.最大公约数
描述
一次生日Party可能有p人或者q人参加,现准备有一个大蛋糕.问最少要将蛋糕切成多少块(每块大小不一定相等),才能使p人或者q人出席的任何一种情况,都能平均将蛋糕分食.
输入
每行有两个数p和q.
输出
输出最少要将蛋糕切成多少块.
样例输入
2 3
样例输出
4
思路&题解
看到题目首先没有理解题意,在蛋糕可以不等大的情况下平均分食是指每个人可以选择不同数量的蛋糕,以达到每个人拥有的蛋糕总量都一样。
但是到这里的时候我没思路了。没有思路就先做不完全归纳,画圆,不难发现当p和q都为偶数时,只需要将蛋糕分成 max{p, q} 个就可以了。接着归纳其他情况,例如p、q为3、5时,先将蛋糕3等分,再想办法5等分,可以发现直接多切2刀是无论如何也无法5等分的,于是多切4刀,总共7刀。推导到这里都还好,但是随着数量增加,仍然只能靠感觉,发现不了规律。于是回头,再次审视我画的这圆圆的蛋糕。
不如,将含有3等分线的蛋糕看做一个轮盘,再将含有5等分线的蛋糕看做一个轮盘,让他们重叠之后旋转。旋转过程中,要保证切的刀数最小,也就是让有些刀尽量即能为3等分做贡献,也为5等分做贡献。于是保证尽可能多的等分线重合。这样,3和5最多有一个线重合。再尝试3和7,最多一条线重合;6和2,最多2条线……稍微思考了一下,一个一个数p的等分线,那么应该是每前进若干个1/p 的时候,就会有一条线与 q 的一个等分线重合, 也就是达到了 1/q. 那么1/p 和 1/q 就应该有比例关系,想起了D题的卫星相遇周期,于是发现,这tm是求gcd(最大公约数)啊!
得到重合线最多个数是gcd(p,q).
代码
1 |
|
K.01背包
描述
首先吐槽出题人的英语水平, 看看题目名吧
Speakless很早就想出国,现在他已经考完了所有需要的考试,准备了所有要准备的材料,于是,便需要去申请学校了。要申请国外的任何大学,你都要交纳一定的申请费用,这可是很惊人的。Speakless没有多少钱,总共只攒了n万美元。他将在m个学校中选择若干的(当然要在他的经济承受范围内)。每个学校都有不同的申请费用a(万美元),并且Speakless估计了他得到这个学校offer的可能性b。不同学校之间是否得到offer不会互相影响。“I NEED A OFFER”,他大叫一声。帮帮这个可怜的人吧,帮助他计算一下,他可以收到至少一份offer的最大概率。(如果Speakless选择了多个学校,得到任意一个学校的offer都可以)。
输入
输入有若干组数据,每组数据的第一行有两个正整数n,m(0<=n<=10000,0<=m<=10000)
后面的m行,每行都有两个数据ai(整型),bi(实型)分别表示第i个学校的申请费用和可能拿到offer的概率。
输入的最后有两个0。
输出
每组数据都对应一个输出,表示Speakless可能得到至少一份offer的最大概率。用百分数表示,精确到小数点后一位。
样例输入
10 3
4 0.1
4 0.2
5 0.3
0 0
样例输出
44.0%
题解
01背包问题。因为至少得到一份offer的概率不能累计,所以将输入中得到offer的概率改为得不到offer的概率存储,然后建立dp数组。定义dp[i]为申请完第0 ~ i 个学校得不到offer的最小概率。则得到状态转移方程:
.其中a[i]是第i个学校的申请费用,b[i]是第i个学校不被录取的概率。(完全就是背包问题嘛)
最后用 1 - min(dp[i]) 就是问题答案。
代码
1 |
|
O.高精
==贴这题只是想提醒一下自己,高精不一定非得写板子写类啊,这题直接用数组作乘法就ok了,不需要额外的对象化。==
V.树的遍历
描述
A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.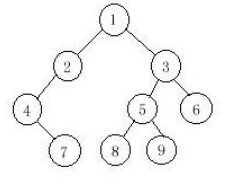
输入
The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.
输出
For each test case print a single line specifying the corresponding postorder sequence.
样例输入
9
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6
样例输出
7 4 2 8 9 5 6 3 1
题解
题意:给定一棵树的先序遍历和中序遍历,求后序遍历。首先通过先序遍历和中序遍历构建树。
先序遍历的第一个数就是树根,在中序遍历中找出这个树根,则树根左右的子序列就是左右子树的中序遍历,而先序遍历的树根之后紧跟着左右子树的先序遍历,由此确定左右子树,以此递归下去。
建树完成后,通过深度优先搜索得到后序遍历. 后序遍历的搜索顺序是:左子树->右子树->根.
代码
1 |
|
其它
做本题的时候紫书进度正好在树这一章节,刚学完从中序和后序遍历求先序遍历。所以这题是此时此刻再合适不过的练习题了~
W.思维
Friend number are defined recursively as follows.
(1) numbers 1 and 2 are friend number;
(2) if a and b are friend numbers, so is ab+a+b;
(3) only the numbers defined in (1) and (2) are friend number.
Now your task is to judge whether an integer is a friend number.
输入
There are several lines in input, each line has a nunnegative integer a, 0<=a<=2^30.
输出
For the number a on each line of the input, if a is a friend number, output “YES!”, otherwise output “NO!”.
样例输入
3
13121
12131
样例输出
YES!
YES!
NO!
题解
像E - Cake那题一样,先不完全归纳一下,1和2是,那么2 + 2 + 1 = 5也是;紧接着 11、 17也是。到这里后我又推了几个,没找着规律。于是回头看公式,ab + a + b,拆成(a + 1)(b + 1) - 1. 发现所有的(a + 1)(b + 1)均为6的倍数!但是特别注意这里a和b也可能相等,而都取1时结果为4、都取2时结果为9,说明3和8也是Friend Number. 进一步,都取3,那(a + 1)(b + 1)的值就是16. 再看取8,得到80.
若干数据之后得出:如果一个数是Friend Number,那么这个数 - 1后必定只有2和3这两个素因子.
做题时不知道是如何证明的,总之稀里糊涂一次AC了,之后看题解知道了证明过程:
设n是不为1也不为2的friend number,那么存在两个friend number a和b,使得 n = ab + a + b.
因式分解得到
既然1和2是最小的两个friend number,而n + 1也仅由其他的friend number决定,不难知道n + 1一定是由2和3乘出的。
代码
1 |
|
DP专题
A.前缀 + dp
描述
Now I think you have got an AC in Ignatius.L’s “Max Sum” problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you are faced with a more difficult problem.
Given a consecutive number sequence S1, S2, S3, S4 … Sx, … Sn (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ Sx ≤ 32767). We define a function sum(i, j) = Si + … + Sj (1 ≤ i ≤ j ≤ n).
Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i1, j1) + sum(i2, j2) + sum(i3, j3) + … + sum(im, jm) maximal (ix ≤ iy ≤ jx or ix ≤ jy ≤ jx is not allowed).
But I`m lazy, I don’t want to write a special-judge module, so you don’t have to output m pairs of i and j, just output the maximal summation of sum(ix, jx)(1 ≤ x ≤ m) instead. ^_^
输入
Each test case will begin with two integers m and n, followed by n integers S1, S2, S3 … Sn.
Process to the end of file.
输出
Output the maximal summation described above in one line.
样例输入
1 3 1 2 3
2 6 -1 4 -2 3 -2 3
样例输出
6
8
题意
给定一个长度为n的数组,从中选m个不相交的子序列,求得到的子序列最大和为多少.
分析
利用dp拆解问题——dp[i][j]表示前j个数分成j组得到的最大和,且保证a[i]在最后一个子序列中。其中i<n,i≤j≤m.
如何进行状态转移?试想,要把dp[i]算出,且保证a[i]在子序列中,只有两种情况:一种是让a[i]自成一个子序列,二是把a[i]加入前面i-1个数的最后一个子序列中。那么状态转移方程为$dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + a[i]$.然后记录dp数组最大值即可。
但题目提示数据规模在百万级别,开数组会内存超限。于是二维数组存dp不可行了。尝试优化,将dp数组的第二维存入一个前缀数组,这样将空间复杂度从O(n^2^)降低到了O(2n),于是设dp[i]为前i个数的答案,然后有一个记录数组fdp,每次i增加时,fdp数组都存储前面i-1个元素中所要求的当前子序列个数-1个子序列最大子段和。到这里无法直接进行划分,故可以外套循环从1至m,依次求出1划分至m划分的答案。
状态转移方程:$dp[i] = max(dp[i-1],fdp[i-1])+a[i]$.
此处dp[i-1]即a[i]接入最后一个序列的情况,fdp[i-1]为a[i]单独成子序列的情况。
特别注意上述方程没有确定子序列个数,需要从1遍历至m不断更新。
^fdp是我瞎取的名字啦^
代码
1 |
|
C.排序 + DP
描述
A group of researchers are designing an experiment to test the IQ of a monkey. They will hang a banana at the roof of a building, and at the mean time, provide the monkey with some blocks. If the monkey is clever enough, it shall be able to reach the banana by placing one block on the top another to build a tower and climb up to get its favorite food.
The researchers have n types of blocks, and an unlimited supply of blocks of each type. Each type-i block was a rectangular solid with linear dimensions (xi, yi, zi). A block could be reoriented so that any two of its three dimensions determined the dimensions of the base and the other dimension was the height.
They want to make sure that the tallest tower possible by stacking blocks can reach the roof. The problem is that, in building a tower, one block could only be placed on top of another block as long as the two base dimensions of the upper block were both strictly smaller than the corresponding base dimensions of the lower block because there has to be some space for the monkey to step on. This meant, for example, that blocks oriented to have equal-sized bases couldn’t be stacked.
Your job is to write a program that determines the height of the tallest tower the monkey can build with a given set of blocks.
输入
The input file will contain one or more test cases. The first line of each test case contains an integer n,
representing the number of different blocks in the following data set. The maximum value for n is 30.
Each of the next n lines contains three integers representing the values xi, yi and zi.
Input is terminated by a value of zero (0) for n.
输出
For each test case, print one line containing the case number (they are numbered sequentially starting from 1) and the height of the tallest possible tower in the format “Case case: maximum height = height”.
Sample Input
1
10 20 30
2
6 8 10
5 5 5
7
1 1 1
2 2 2
3 3 3
4 4 4
5 5 5
6 6 6
7 7 7
5
31 41 59
26 53 58
97 93 23
84 62 64
33 83 27
0
Sample Output
Case 1: maximum height = 40
Case 2: maximum height = 21
Case 3: maximum height = 28
Case 4: maximum height = 342
题意
给n种长方体,每种长方体无限个,将他们摞起来,保证下面的长&宽分别严格大于上面的长&宽。其中每一个长方体都可以改变朝向。
分析
因为可以换朝向,所以把三个数字对长-宽-高的排列全放进去(也就是每个输入其实相当于放了6种长方体进数组)。直接设dp[i][j]为把第i种放在第j层的答案,不过由于状态转移方程一时半会写不出+感觉时间空间都比较复杂,于是摒弃了这种设计。另起炉灶:
先贪心排序,不考虑高,按长更大优先排序,长相等的按宽更大优先排序,这样数组从前往后可以保证答案的长方体序列的顺序一定是从前往后,不会出现交叉。然后设dp[i]为前i个长方体的答案,类似于求递增子列的最大和。对每个dp[i],枚举dp[0]~dp[i-1],如果第i个可以摞在第j个上面,且摞起来之后的高度大于原本的dp[i],就更新dp[i]。状态转移方程为$dp[i] = max(dp[i], dp[j] + height[i])(j<i,length[i]<length[j],width[i]<width[j])$.
两层循环,平方复杂度。
代码
1 |
|
J.排序 + DP
结构体先排序再dp,和C一模一样的套路,不过多了记录答案的具体序列,用一个类链表的数组记录序列前一个的位置即可,只贴代码和链接。
1 |
|
L.最大公共子序列
(以后题解的题面就直接复制OJ上的吧,自己打题面的格式没啥意义哈哈哈)
description
A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = < x1, x2, …, xm > another sequence Z = < z1, z2, …, zk > is a subsequence of X if there exists a strictly increasing sequence < i1, i2, …, ik > of indices of X such that for all j = 1,2,…,k, xij = zj. For example, Z = < a, b, f, c > is a subsequence of X = < a, b, c, f, b, c > with index sequence < 1, 2, 4, 6 >. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.
Input
The program input is from the std input. Each data set in the input contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct.
Output
For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
Sample Input
1 | abcfbc abfcab |
Sample Output
1 | 4 |
题意
求两个字母字符串的最大公共子序列(注意不是子串)。
分析
用二维表存储dp结果。dp[i][j]表示第一个串的前i个和第二个串的前j个构成的子答案。
如果a串的第i个和b串的第j个字母相同,那么dp[i][j] = dp[i - 1][j - 1] + 1.
否则的话,只能继承之前的最佳答案了,dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]).
代码
1 |
|
Q.二维DP
description
Today is army day, but the servicemen are busy with the phalanx for the celebration of the 60th anniversary of the PRC.
A phalanx is a matrix of size nn, each element is a character (a~z or A~Z), standing for the military branch of the servicemen on that position.
For some special requirement it has to find out the size of the max symmetrical sub-array. And with no doubt, the Central Military Committee gave this task to ALPCs.
A symmetrical matrix is such a matrix that it is symmetrical by the “left-down to right-up” line. The element on the corresponding place should be the same. For example, here is a 33 symmetrical matrix:
cbx
cpb
zcc
Input
There are several test cases in the input file. Each case starts with an integer n (0<n<=1000), followed by n lines which has n character. There won’t be any blank spaces between characters or the end of line. The input file is ended with a 0.
Output
Each test case output one line, the size of the maximum symmetrical sub- matrix.
Sample Input
1 | 3 |
Sample Output
1 | 3 |
题意
给一个字符方阵,把副对角线当对称轴,求最大的对称子方阵。
分析
设dp[i][j]表示a[i][j]为某个对称方阵左下角的字符时最大对称子方阵的大小。由于自己肯定是个对称方阵,初始化所有的dp[i][j]为1.
接着如果dp[i-1][j+1]为k,那么我们要检查a[i][j]上面那一列和右边那一行是否分别相等即可。检查1到k个,每次符合就dp[i][j]++,不符合就break.
代码
1 |
|